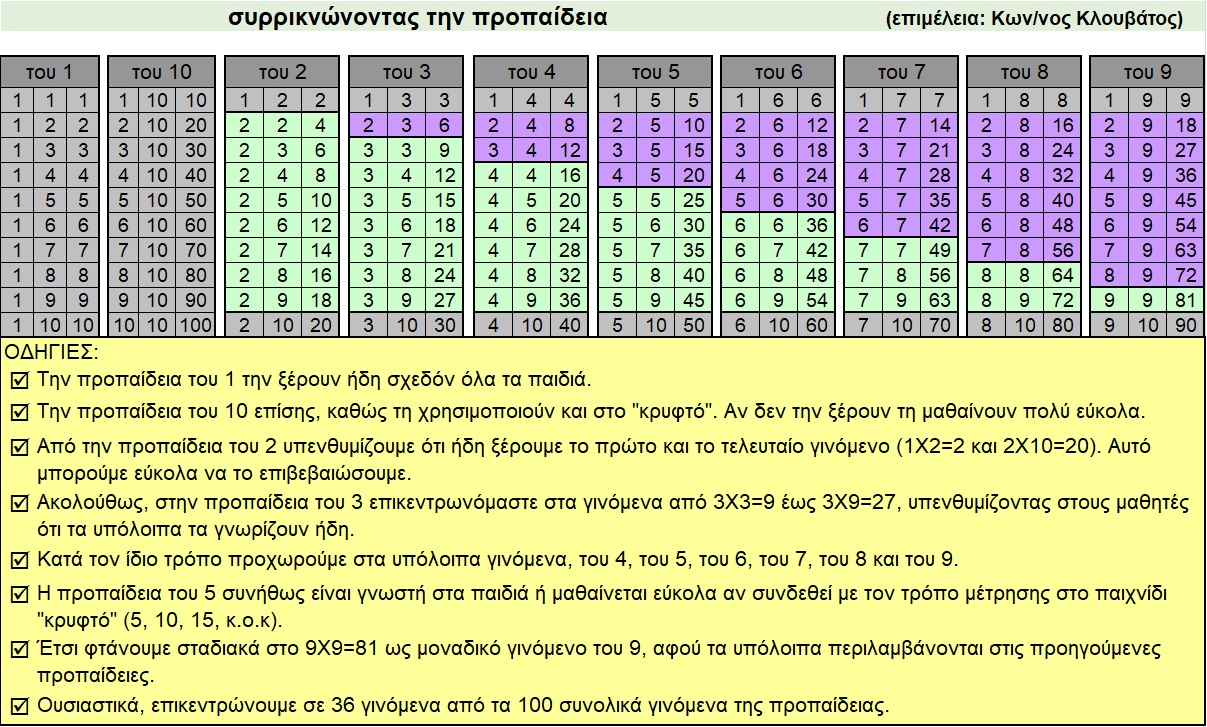
Α. Η προπαίδεια σε πολύ πιο σύντομη και εύκολη μορφή
[απαιτείται η εκμάθηση μόνο των 36 γινομένων που βρίσκονται στα ανοιχτόχρωμα (λαχανί) κελιά του πίνακα]
Β. Πρόσθετες προτάσεις διδασκαλίας της προπαίδειας
-
Η επιλογή του τρόπου εκμάθησης στης προπαίδειας μπορεί να είναι καθοριστική. Κάποιοι διδάσκουν την προπαίδεια με μακροσκελή μορφή, π.χ. στην προπαίδεια του 2 λένε: 1 φορά το 2 ίσον 2, 2 φορές το 2 ίσον 4, 3 φορές το 2 ίσον 6 κ.ο.κ. ή λένε 1 φορά το 2 : 2, 2 φορές το 2 : 4 κ.ο.κ. Βασικές παρατηρήσεις εδώ είναι ότι::
-
(α) ακόμη και η πιο σύντομη μορφή "1 φορά το 2: 2", "2 φορές το 2: 4" κ.ο.κ. είναι περίπλοκη και χρονοβόρα. Προτείνεται η ακόμη πιο συντομευμένη μορφή "1 οι 2: 2" (μία οι δύο...δύο), "2 οι 2: 4" (δύο οι δύο ...τέσσερα) κ.ο.κ. Με τον τρόπο αυτό μπερδεύονται λιγότερο οι μαθητές, όπως έχει δείξει η πολύχρονη εμπειρία εκπαιδευτικών και μαθητών. Κάποιοι, πάριν συντομίας, παραλείπουν ακόμα και το "οι" που παρεμβάλλεται μεταξύ των όρων των γινομένων λέγοντας "μία δύο δύο, πέντε έξι τριάντα κ.ο.κ.
-
(β) η μορφή της προπαίδειας που θέτει ως πρώτο όρο του γινομένου πάντοτε τον μικρότερο αριθμό, όπως π.χ. στην προπαίδεια του 2: "2 οι 3: 6", "2 οι 6: 12", ..."2 οι 8: 16" κ.ο.κ., φαίνεται να είναι ευκολότερα κατανοητή από το ανθρώπινο μυαλό από τη μορφή "6 οι 2" ή "9 οι 2" κ.ο.κ. Κι αυτό γιατί πολύ πιο εύκολα αντιλαμβάνεται και υπολογίζει κανείς 2 εννιάδες παρά 9 δυάδες, 3 12άδες παρά 12 3άδες κ.ο.κ. Στη δεύτερη περίπτωση οι περισσότεροι αναγκάζονται να κάνουν μια νοερή αντιστροφή της σειράς των αριθμών και υπολογίζουν τελικά 3 εννιάδες αντί 9 τριάδες. Συνεπώς, προτείνεται η προσαρμοσμένη (παλαιότερη) μορφή της προπαίδειας που παρουσιάζεται στον παραπάνω πίνακα.
-
(γ) η αισθητοποίηση τών μικρών γινομένων μπορεί να γίνει αβίαστα με κάρτες όπως τα τραπουλόχαρτα που σχηματοποιούν τα γινόμενα. Αν είμαστε επιφυλακτικοί με τη χρήση τράπουλας στα παιδιά, μπορούμε να φτιάξουμε εύκολα ή να βρούμε στο εμπόριο παρόμοιες κάρτες. Εξάλλου, η κοινή τράπουλα μπορεί να χρησισμοποιηθεί μόνο σε μικρούς αριθμούς (μέχρι το 10). Παίζοντας με τέτοιες κάρτες, οι παίχτες αντιλαμβάνονται και οπτικά τους επιμέρους όρους του γινομένου και του αθροίσματος που απαρτίζουν τους αριθμούς. Επίσης, αντιλαμβάνονται ευκολότερα την αντιμεταθετική ιδιότητα (π.χ. 5 Χ 6 = 6 Χ 5). Αν αφαιρεθούν εν ευθέτω χρόνω τα σύμβολα των αριθμών από τις κάρτες, οι παίχτες θα μπορούν να βρίσκουν γρήγορα τον αριθμό που κρύβεται πίσω από το εικονιζόμενο γινόμενο. Για τον ίδιο σκοπό χρησιμοποιούνται και τα ζάρια.
-
Σε κάθε περίπωση, το μεγάλο ζητούμενο για κάθε άνθρωπο παραμένει ή αυτοματοποίηση της προπαίδειας κάποια στιγμή, δηλαδή να μπορεί κανείς να βρίσκει αμέσως οποιοδήποτε γινόμενο, χωρίς τη χρήση βοηθημάτων (εικόνων, καρτών, δαχτύλων κ.ο.κ.).
-



Βρείτε έτοιμα φύλλα εργασίας ή πάρτε ιδέες για να φτιάξετε κάρτες με εικονίδια για την προπαίδεια στα:
Γ. Χωροθετώντας τα γινόμενα της προπαίδειας
Για κάποιον που δυσκολεύεται στην εκμάθηση της προπαίδειας, η χωροθέτηση των γινομένων μπορεί να αποδειχθεί εξόχως βοηθητική.
Βασικές παρατηρήσεις είναι οι εξής:
-
Όλα τα γινόμενα του πίνακα της προπαίδειας είναι διπλά, δηλαδή περιλαμβάνονται σε δυο προπαίδειες. Έχοντάς το αυτό υπόψη μπορεί κάποιος να διευκολυνθεί από τη νοερή ή γραπτή αντιστροφή των όρων του γινομένου.
Π.χ. το 7 Χ 6 = 42 ίσως υπολογίζεται ευκολότερα ως 6 Χ 7 = 42.
-
Αν πολλαπλασιάζω πολύ μικρούς αριθμούς (1 - 5), αναμένω το γινόμενό τους να είναι χαμηλά στις δύο πρώτες δεκάδες. Όσο πιο μικροί είναι οι δυο αριθμοί μου, τόσο πιο χαμηλά θα βρίσκεται το γινόμενό τους.
Παραδείγματα: 2 Χ 4 = 8, 3 Χ 4 = 12, 4 Χ 5 = 20 κ.ο.κ. Μόνο το 5 Χ 5 = 25 βρίσκεται στην τρίτη δεκάδα.
-
Πάνω από το 50 έχω να μάθω μόνο 6 γινόμενα μεγάλων αριθμών (6, 7, 8 και 9), τα εξής: 6 Χ 9 = 54, 7 Χ 8 = 56, 7 Χ 9 = 63, 8 Χ 8 = 64, 8 Χ 9 = 72, 9 Χ 9 = 81.
-
Στα 6 παραπάνω γινόμενα παρατηρούμε τα εξής:
-
Στη δεκάδα 50-60 έχουμε δύο γειτονικά γινόμενα, τα 6 Χ 9 = 54 και 7 Χ 8 = 56. Παρατηρόυμε ότι οι αριθμοί 7 και 8, οι οποίοι είναι ανάμεσα στους 6 και 9, δίνουν ελαφρώς μεγαλύτερο γινόμενο: 7 Χ 8 = 56 έναντι 6 Χ 9 = 54.
-
Στη δεκάδα 60-70 έχουμε και πάλι δύο γειτονικά γινόμενα, τα 7 Χ 9 = 63 και 8 Χ 8 = 64. Παρατηρούμε κι εδώ ότι οι αριθμοί 8 και 8, οι οποίοι βρίσκονται ανάμεσα στους 7 και 9, δίνουν ελαφρώς μεγαλύτερο γινόμενο: 8 Χ 8 = 64 έναντι 7 Χ 9 = 63.
-
Στη δεκάδα 70-80 έχουμε ένα μόνο γινόμενο, το 8 Χ 9 = 72 και
-
Στη δεκάδα 80-90 έχουμε ένα μόνο γινόμενο το 9 Χ 9 = 81.
-
-
Γενικότερα, παρατηρούμε ότι δυο αριθμοί που είναι ανάμεσα σε δυο άλλους αριθμούς δίνουν μεγαλύτερο γινόμενο. Παραδείγματα: (α) 6 Χ 6 = 36 ενώ 5 Χ 7 = 35. (β) Οι αριθμοί 5 Χ 8 έχουν έχουν ελαφρώς μικρότερο γινόμενο (40) από το γινόμενο των ενδιάμεσων αριθμών 6 Χ 7 (42).
-
Στην παρακάτω εικόνα παρουσιάζεται η χωροθεσία των γινομένων της προπαίδειας στις δεκάδες:

Δ. Άλλα γινόμενα που αξίζει να αυτοματοποιήσει κανείς
Σε πολλά εκπαιδευτικά συστήματα η προπαίδεια δε σταματά στο 10, αλλά στο 12. Θεωρητικά η προπαίδεια δε σταματά ποτέ. Επειδή όμως ο ανθρώπινος νους δεν μπορεί, ούτε χρειάζεται, να αποστηθίζει τα πάντα - γι' αυτό εξάλλου μαθαίνουμε να κάνουμε πολλαπλασιασμό και να χρησιμοποιούμε αριθμομηχανή (κομπιουτεράκι) - κρίνεται σκόπιμη η αυτοματοποίηση μερικών ακόμη συχνόχρηστων γινομένων. Κι αυτό επειδή μεγαλώνοντας συναντούμε όλο και πιο συχνά τέτοια γινόμενα, για τα οποία θα ήταν χάσιμο χρόνου να κάνουμε πράξεις για να τα βρίσκουμε. Ποια είναι αυτά τα γινόμενα;
-
Κάποιοι μαθαίνουν ολόκληρη την προπαίδεια του 11 και του 12. Εμείς προτείνουμε τα εξής:
-
Η προπαίδεια του 11 είναι η πιο εύκολη προπαίδεια μετά την προπαίδεια του 1 και του 10, διότι 1 Χ 11 = 11, 2 Χ 11 = 22, ....7 Χ 11 = 77 κ.ο.κ. Παρατηρούμε δηλαδή ότι όταν πολλαπλασιάζουμε με το 11 βρίσκουμε διπλό το ψηφίο με το οποίο το πολλαπλασιάζουμε. Δηλαδή, πολλαπλασιάζουμε το 11 με το 4 και βρίσκουμε 44, με το 8 και βρίσκουμε 88 κ.ο.κ. Προσοχή στο 10 Χ 11 που μας κάνει 110.
-
Από την προπαίδεια του 12 καλό θα ήταν να αυτοματοποιήσουμε τα πρώτα γινόμενα, που θα τα συναντούμε συχνά: 1 Χ 12 = 12, 2 Χ 12 = 24, 3 Χ 12 = 36, 4 Χ 12 = 48, 5 Χ 12 = 60, 6 Χ 12 = 72. Τα υπόλοιπα γινόμενα ας τα βρίσκουμε με πολλαπλασιασμό.
-
Από την προπαίδεια του 13 καλό θα ήταν να αυτοματοποιήσουμε τα εξής γινόμενα: 1 Χ 13 = 13, 2 Χ 13 = 26, 3 Χ 13 = 39, 4 Χ 13 = 52. Τα γινόμενα αυτά έχουν σχέση και με 4 χρώματα (καρό, σπαθί, κούπα και μπαστούνι) των 52 τραπουλόχαρτων, τα οποία υπάρχουν 13 φορές μέσα στην τράπουλα.
-
Από την προπαίδεια του 15 πρέπει να αυτοματοποιήσουμε οπωσδήποτε τα εξής γινόμενα: 1 Χ 15 = 15, 2 Χ 15 = 30, 3 Χ 15 = 45, 4 Χ 15 = 60, γιατί τα συναντάμε πολύ συχνά σε προβλήματα. Κάποιοι έχουν αποστηθίσει και τα μεγαλύτερα 5 Χ 15 = 75 και 6 Χ 15 = 90.
-
Από την προπαίδεια του 16 καλό είναι να αυτοματοποιήσουμε τα γινόμενα: 1 Χ 16 = 16, 2 Χ 16 = 32, 3 Χ 16 = 48, 4 Χ 16 = 64, μιας και τα συναντάμε επίσης πολύ συχνά σε προβλήματα.
-
Την προπαίδεια του 20 τη γνωρίζουμε ήδη από την προπαίδεια του 2. Με πολύ λίγη εξάσκηση αυτοματοποιείται εύκολα: 3 Χ 20 = 60 όπως 2 Χ 3 = 6, 6 Χ 20 = 120 όπως 2 Χ 6 = 12 κ.ο.κ.
-
Κατά τον ίδιο τρόπο αυτοματοποιούμε την προπαίδεια του 30, 40, 50, 60, 70, 80, 90. Για ευκολία μπορούμε να λέμε την προπαίδεια του 2, 3, 4, 5, κ.ο.κ. και στο τέλος να προσθέτουμε ένα μηδενικό. Π.χ. αντί για 3 Χ 60 = 180, λέμε 3 Χ 6 = 18 και βάζουμε στο τέλος του 18 το 0, δηλαδή 180.
-
Από την προπαίδεια του 25 θα μας βοηθήσει πολύ η αυτοματοποίηση των πρώτων γινομένων, καθώς θα τα βρίσκουμε συνεχώς μπροστά μας: 1 Χ 25 = 25, 2 Χ 25 = 50, 3 Χ 25 = 75, 4 Χ 25 = 100, 5 Χ 25 = 125.
-
Από την προπαίδεια των υπόλοιπων διψήφιων, δηλαδή του 14, του 17, 18, 19, ως το 49, καλό είναι να μπορούμε να βρίσκουμε αμέσως τουλάχιστον τα διπλάσιά τους, π.χ. 2 Χ 48 = 92 ή 2 Χ 37 = 74 κ.ο.κ. Για τα διπλάσια των υπόλοιπων διψήφιων από 51 ως 99 εργαζόμαστε με τον ίδιο τρόπο. Ωστόσο, κάποια από αυτά είναι λίγο πιο πολύπλοκα, όπως αυτά που έχουν μονάδες πάνω από 5. Π.χ. στο γινόμενο 2 Χ 76 δεν αρκεί να διπλασιάσουμε με το μυαλό μας το 70 (2 Χ 70 = 140), αλλά ταυτόχρονα να διπλασιάσουμε και το 6 (2 Χ 6 = 12) και μετά να πούμε νοερώς: 140 + 12 = 152. Η αυτοματοποίηση σε αυτά τα γινόμενα θα έρθει εν καιρώ, ανάλογα με την πρόοδο που έχει συντελεστεί στα προηγούμενα γινόμενα και στην νοερή πρόσθεση διψήφιων αριθμών, π.χ. 87 + 87 = 174.
-
Ανεβαίνοντας ακόμη ψηλότερα, εύκολα αυτοματοποιούμε την προπαίδεια του 100 και με λίγο μεγαλύτερη εξάσκηση την προπαίδεια των υπόλοιπων εκατοντάδων, του 200, του 300 κ.ο.κ., επειδή τα γινόμενά τους υπερβαίνουν το 1.000.
-
Με την ίδια λογική αυτοματοποιούμε τα πρώτα τουλάχιστον γινόμενα του 250, όπως του 25, του 500, του 1.000 κ.ο.κ.
-
-
Θεωρητικκά μπορούμε να ανεβαίνουμε όσο ψηλά θέλουμε στην αριθμητική κλίμακα χωρίς να νιώθουμε ότι "τρομάζουμε" τα μικά παιδιά. Συνήθως τα παιδιά απολαμβάνουν και επιζητούν αυτή την αριθμητική "αναρρίχηση", αποβάλλουν κάθε πιθανή φοβία για τους μεγάλους αριθμούς και αντιλαμβάνονται ότι οι νόμοι των μαθηματικών παραμένουν εύκολοι, απλοί και ίδιοι όσο ψηλά και αν ανεβούμε στην αριθμητική κλίμακα. π.χ. 3 Χ 5 = 15 και 3 Χ 5.000 = 15.000 κ.ο.κ.
-
Σε κάθε περίπτωση, πρέπει να χτίσουμε γερά θεμέλια στην πρώτη δεκάδα και την πρώτη εκατοντάδα. Μετά όλα εξελίσσονται κατ' ευχήν.
Ta γινόμενα 6Χ6 έως 9Χ9 με πανεύκολο τρόπο
H προπαίδεια του 9 πανεύκολα:
Πολλαπλασιάζοντας εύκολα γινόμενα από 11 Χ 11 έως 19 Χ 19
Πολλαπλασιάζοντας εύκολα και γρήγορα διψήφιους αριθμούς με το 11
Εναλλακτικοί τρόποι πολλαπλασιασμού
Πολλαπλασιάζοντας εύκολα κατά τον κινεζικό (ή αρχαιοελληνικό;) τρόπο
Η ιαπωνική εκδοχή του εύκολου πολλαπλασιασμού
Περισσότερη εξάσκηση στην προπαίδεια:
http://www.learnyourtables.co.uk/gk/index.htm
http://e-math.eduportal.gr/efarmoges/xion.htm
http://11dim-evosm.thess.sch.gr/downloads/proper.xls
Απλή δοκιμασία προπαίδειας (προσαρμόσιμη)
Ακόμη περισσότερη εξάσκηση στην προπαίδεια εδώ (από το http://users.sch.gr/tasisp/index.swf)
https://www.mathplayground.com/index_multiplication_division.html
Αγώνας
ταχύτητας με προπαίδεια για απαιτητικούς παίχτες:
http://www.arcademicskillbuilders.com/games/grand_prix/grand_prix.html

Καταστροφή μετεωριτών με προπαίδεια:
http://www.arcademicskillbuilders.com/games/meteor/meteor.html